diffeqr

Solving differential equations in R using DifferentialEquations.jl and the SciML Scientific Machine Learning ecosystem

116

diffeqr

diffeqr is a package for solving differential equations in R. It utilizes
DifferentialEquations.jl for its core routines
to give high performance solving of ordinary differential equations (ODEs),
stochastic differential equations (SDEs), delay differential equations (DDEs), and
differential-algebraic equations (DAEs) directly in R.

If you have any questions, or just want to chat about solvers/using the package,
please feel free to chat in the Zulip channel. For bug reports, feature requests, etc., please submit an issue.

Installation

diffeqr is registered into CRAN. Thus to add the package, use:

install.packages("diffeqr")

To install the master branch of the package (for developers), use:

devtools::install_github('SciML/diffeqr', build_vignettes=T)

Note that the first invocation of
diffeqr::diffeq_setup() will install both Julia
and the required packages if they are missing.
If you wish to have it use an existing Julia binary,
make sure that julia is found in the path. For more
information see the julia_setup() function from
JuliaCall.

Google Collab Notebooks

As a demonstration, check out the following notebooks:

Usage

diffeqr provides a direct wrapper over DifferentialEquations.jl.
The namespace is setup so that the standard syntax of Julia translates directly
over to the R environment. There are two things to keep in mind:

All DifferentialEquations.jl commands are prefaced by de$
All commands with a ! are replaced with _bang, for example solve! becomes solve_bang.

Ordinary Differential Equation (ODE) Examples

1D Linear ODEs

Let’s solve the linear ODE u'=1.01u. First setup the package:

de <- diffeqr::diffeq_setup()

Define the derivative function f(u,p,t).

f <- function(u,p,t) {
  return(1.01*u)
}

Then we give it an initial condition and a time span to solve over:

u0 <- 1/2
tspan <- c(0., 1.)

With those pieces we define the ODEProblem and solve the ODE:

prob = de$ODEProblem(f, u0, tspan)
sol = de$solve(prob)

This gives back a solution object for which sol$t are the time points
and sol$u are the values. We can treat the solution as a continuous object
in time via

sol$.(0.2)

and a high order interpolation will compute the value at t=0.2. We can check
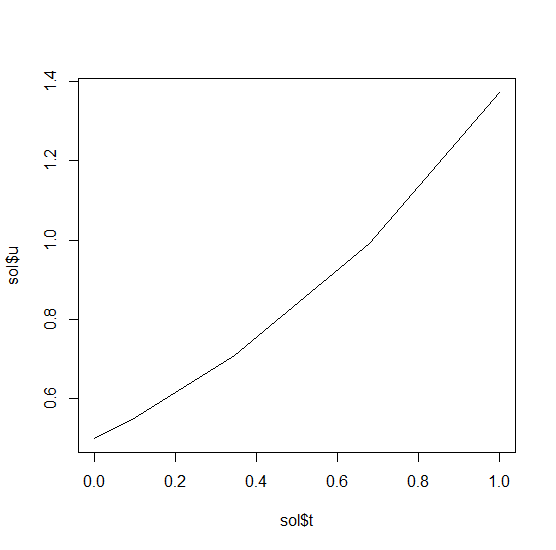
the solution by plotting it:

plot(sol$t,sol$u,"l")

linear_ode

Systems of ODEs

Now let’s solve the Lorenz equations. In this case, our initial condition is a vector and our derivative functions
takes in the vector to return a vector (note: arbitrary dimensional arrays are allowed). We would define this as:

f <- function(u,p,t) {
  du1 = p[1]*(u[2]-u[1])
  du2 = u[1]*(p[2]-u[3]) - u[2]
  du3 = u[1]*u[2] - p[3]*u[3]
  return(c(du1,du2,du3))
}

Here we utilized the parameter array p. Thus we use diffeqr::ode.solve like before, but also pass in parameters this time:

u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(f, u0, tspan, p)
sol <- de$solve(prob)

The returned solution is like before except now sol$u is an array of arrays,
where sol$u[i] is the full system at time sol$t[i]. It can be convenient to
turn this into an R matrix through sapply:

mat <- sapply(sol$u,identity)

This has each row as a time series. t(mat) makes each column a time series.
It is sometimes convenient to turn the output into a data.frame which is done
via:

udf <- as.data.frame(t(mat))

Now we can use matplot to plot the timeseries together:

matplot(sol$t,udf,"l",col=1:3)

timeseries

Now we can use the Plotly package to draw a phase plot:

plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')

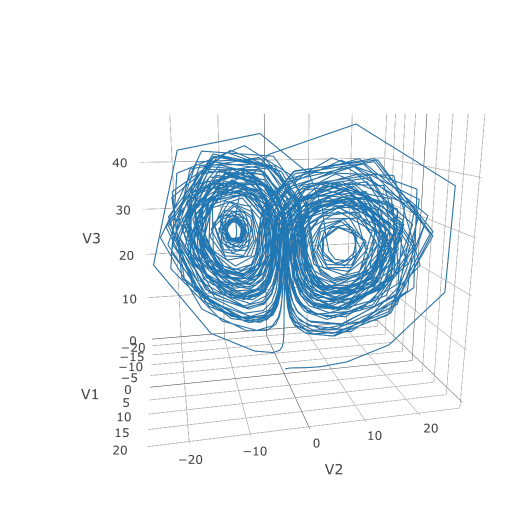
plotly_plot

Plotly is much prettier!

Option Handling

If we want to have a more accurate solution, we can send abstol and reltol. Defaults are 1e-6 and 1e-3 respectively.
Generally you can think of the digits of accuracy as related to 1 plus the exponent of the relative tolerance, so the default is
two digits of accuracy. Absolute tolernace is the accuracy near 0.

In addition, we may want to choose to save at more time points. We do this by giving an array of values to save at as saveat.
Together, this looks like:

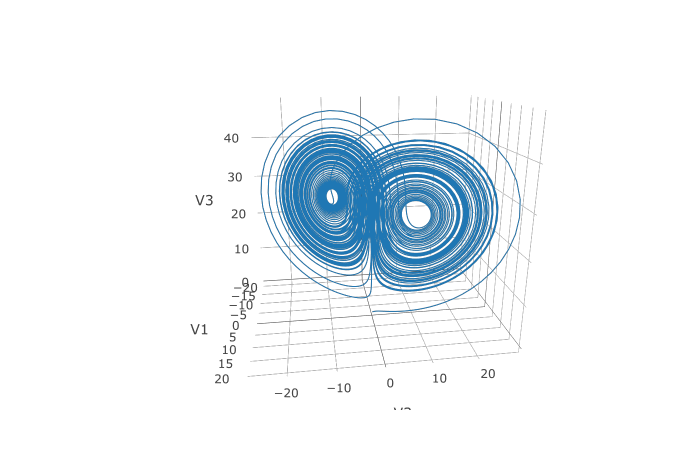
abstol <- 1e-8
reltol <- 1e-8
saveat <- 0:10000/100
sol <- de$solve(prob,abstol=abstol,reltol=reltol,saveat=saveat)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')

precise_solution

We can also choose to use a different algorithm. The choice is done using a string that matches the Julia syntax. See
the ODE tutorial for details.
The list of choices for ODEs can be found at the ODE Solvers page.
For example, let’s use a 9th order method due to Verner:

sol <- de$solve(prob,de$Vern9(),abstol=abstol,reltol=reltol,saveat=saveat)

Note that each algorithm choice will cause a JIT compilation.

Performance Enhancements

One way to enhance the performance of your code is to define the function in Julia
so that way it is JIT compiled. diffeqr is built using
the JuliaCall package, and so
you can utilize the Julia JIT compiler. We expose this automatically over ODE
functions via jitoptimize_ode, like in the following example:

f <- function(u,p,t) {
  du1 = p[1]*(u[2]-u[1])
  du2 = u[1]*(p[2]-u[3]) - u[2]
  du3 = u[1]*u[2] - p[3]*u[3]
  return(c(du1,du2,du3))
}
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(f, u0, tspan, p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)
sol <- de$solve(fastprob,de$Tsit5())

Note that the first evaluation of the function will have an ~2 second lag since
the compiler will run, and all subsequent runs will be orders of magnitude faster
than the pure R function. This means it’s great for expensive functions (ex. large
PDEs) or functions called repeatedly, like during optimization of parameters.

We can also use the JuliaCall functions to directly define the function in Julia
to eliminate the R interpreter overhead and get full JIT compilation:

julf <- JuliaCall::julia_eval("
function julf(du,u,p,t)
  du[1] = 10.0*(u[2]-u[1])
  du[2] = u[1]*(28.0-u[3]) - u[2]
  du[3] = u[1]*u[2] - (8/3)*u[3]
end")
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("p", p)
JuliaCall::julia_assign("tspan", tspan)
prob3 = JuliaCall::julia_eval("ODEProblem(julf, u0, tspan, p)")
sol = de$solve(prob3,de$Tsit5())

To demonstrate the performance advantage, let’s time them all:

> system.time({ for (i in 1:100){ de$solve(prob    ,de$Tsit5()) }})
   user  system elapsed
   6.69    0.06    6.78
> system.time({ for (i in 1:100){ de$solve(fastprob,de$Tsit5()) }})
   user  system elapsed
   0.11    0.03    0.14
> system.time({ for (i in 1:100){ de$solve(prob3   ,de$Tsit5()) }})
   user  system elapsed
   0.14    0.02    0.15

This is about a 50x improvement!

Limitations of the JIT Compilation

Using Julia’s ModelingToolkit
for tracing to JIT compile via Julia has a few known limitations:

It requires that all of the function calls are tracable. Scalar functions
like cos and sin all fall into this category. Notably, matrix multiplication
is not supported.
It will have a compilation lag on the first call.

Stochastic Differential Equation (SDE) Examples

1D SDEs

Solving stochastic differential equations (SDEs) is the similar to ODEs. To solve an SDE, you use diffeqr::sde.solve and give
two functions: f and g, where du = f(u,t)dt + g(u,t)dW_t

de <- diffeqr::diffeq_setup()
f <- function(u,p,t) {
  return(1.01*u)
}
g <- function(u,p,t) {
  return(0.87*u)
}
u0 <- 1/2
tspan <- c(0.0,1.0)
prob <- de$SDEProblem(f,g,u0,tspan)
sol <- de$solve(prob)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = sol$t, y = sol$u, type = 'scatter', mode = 'lines')

geometric_sdes

Systems of Diagonal Noise SDEs

Let’s add diagonal multiplicative noise to the Lorenz attractor. diffeqr defaults to diagonal noise when a system of
equations is given. This is a unique noise term per system variable. Thus we generalize our previous functions as
follows:

f <- function(u,p,t) {
  du1 = p[1]*(u[2]-u[1])
  du2 = u[1]*(p[2]-u[3]) - u[2]
  du3 = u[1]*u[2] - p[3]*u[3]
  return(c(du1,du2,du3))
}
g <- function(u,p,t) {
  return(c(0.3*u[1],0.3*u[2],0.3*u[3]))
}
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,1.0)
p <- c(10.0,28.0,8/3)
prob <- de$SDEProblem(f,g,u0,tspan,p)
sol <- de$solve(prob,saveat=0.005)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')

Using a JIT compiled function for the drift and diffusion functions can greatly enhance the speed here.
With the speed increase we can comfortably solve over long time spans:

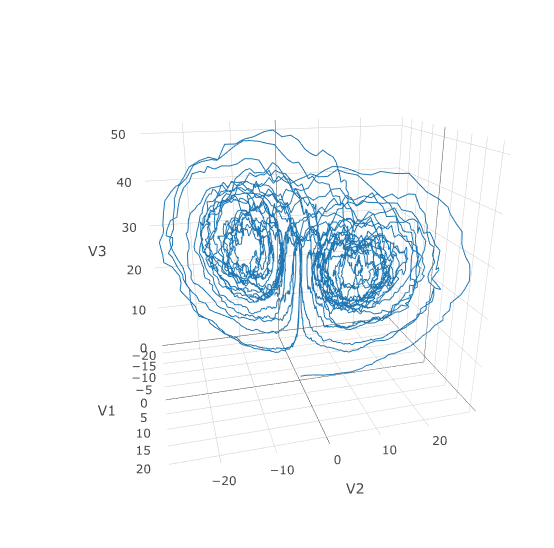
tspan <- c(0.0,100.0)
prob <- de$SDEProblem(f,g,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_sde(de,prob)
sol <- de$solve(fastprob,saveat=0.005)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')

stochastic_lorenz

Let’s see how much faster the JIT-compiled version was:

> system.time({ for (i in 1:5){ de$solve(prob    ) }})
   user  system elapsed
 146.40    0.75  147.22
> system.time({ for (i in 1:5){ de$solve(fastprob) }})
   user  system elapsed
   1.07    0.10    1.17

Holy Monster’s Inc. that’s about 145x faster.

Systems of SDEs with Non-Diagonal Noise

In many cases you may want to share noise terms across the system. This is known as non-diagonal noise. The
DifferentialEquations.jl SDE Tutorial
explains how the matrix form of the diffusion term corresponds to the summation style of multiple Wiener processes. Essentially,
the row corresponds to which system the term is applied to, and the column is which noise term. So du[i,j] is the amount of
noise due to the jth Wiener process that’s applied to u[i]. We solve the Lorenz system with correlated noise as follows:

f <- JuliaCall::julia_eval("
function f(du,u,p,t)
  du[1] = 10.0*(u[2]-u[1])
  du[2] = u[1]*(28.0-u[3]) - u[2]
  du[3] = u[1]*u[2] - (8/3)*u[3]
end")
g <- JuliaCall::julia_eval("
function g(du,u,p,t)
  du[1,1] = 0.3u[1]
  du[2,1] = 0.6u[1]
  du[3,1] = 0.2u[1]
  du[1,2] = 1.2u[2]
  du[2,2] = 0.2u[2]
  du[3,2] = 0.3u[2]
end")
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,100.0)
noise_rate_prototype <- matrix(c(0.0,0.0,0.0,0.0,0.0,0.0), nrow = 3, ncol = 2)

JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("tspan", tspan)
JuliaCall::julia_assign("noise_rate_prototype", noise_rate_prototype)
prob <- JuliaCall::julia_eval("SDEProblem(f, g, u0, tspan, p, noise_rate_prototype=noise_rate_prototype)")
sol <- de$solve(prob)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')

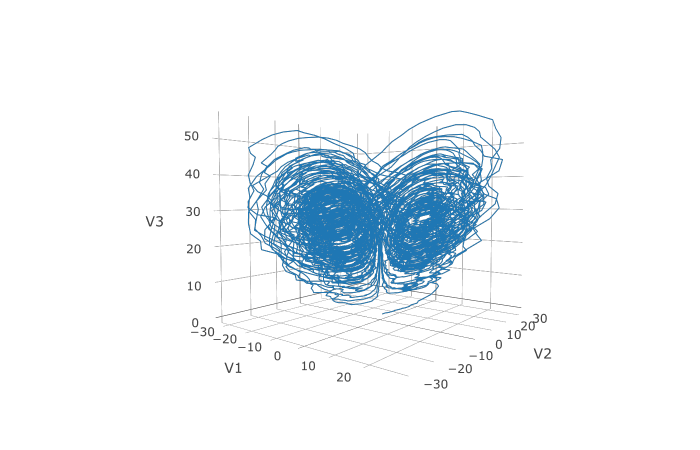
noise_corr

Here you can see that the warping effect of the noise correlations is quite visible!
Note that we applied JIT compilation since it’s quite necessary for any difficult
stochastic example.

Differential-Algebraic Equation (DAE) Examples

A differential-algebraic equation is defined by an implicit function f(du,u,p,t)=0. All of the controls are the
same as the other examples, except here you define a function which returns the residuals for each part of the equation
to define the DAE. The initial value u0 and the initial derivative du0 are required, though they do not necessarily
have to satisfy f (known as inconsistent initial conditions). The methods will automatically find consistent initial
conditions. In order for this to occur, differential_vars must be set. This vector states which of the variables are
differential (have a derivative term), with false meaning that the variable is purely algebraic.

This example shows how to solve the Robertson equation:

f <- function (du,u,p,t) {
  resid1 = - 0.04*u[1]              + 1e4*u[2]*u[3] - du[1]
  resid2 = + 0.04*u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
  resid3 = u[1] + u[2] + u[3] - 1.0
  c(resid1,resid2,resid3)
}
u0 <- c(1.0, 0, 0)
du0 <- c(-0.04, 0.04, 0.0)
tspan <- c(0.0,100000.0)
differential_vars <- c(TRUE,TRUE,FALSE)
prob <- de$DAEProblem(f,du0,u0,tspan,differential_vars=differential_vars)
sol <- de$solve(prob)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |>
  plotly::add_trace(y = ~V2) |>
  plotly::add_trace(y = ~V3)

Additionally, an in-place JIT compiled form for f can be used to enhance the speed:

f = JuliaCall::julia_eval("function f(out,du,u,p,t)
  out[1] = - 0.04u[1]              + 1e4*u[2]*u[3] - du[1]
  out[2] = + 0.04u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
  out[3] = u[1] + u[2] + u[3] - 1.0
end")
u0 <- c(1.0, 0, 0)
du0 <- c(-0.04, 0.04, 0.0)
tspan <- c(0.0,100000.0)
differential_vars <- c(TRUE,TRUE,FALSE)
JuliaCall::julia_assign("du0", du0)
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("p", p)
JuliaCall::julia_assign("tspan", tspan)
JuliaCall::julia_assign("differential_vars", differential_vars)
prob = JuliaCall::julia_eval("DAEProblem(f, du0, u0, tspan, p, differential_vars=differential_vars)")
sol = de$solve(prob)

daes

Delay Differential Equation (DDE) Examples

A delay differential equation is an ODE which allows the use of previous values. In this case, the function
needs to be a JIT compiled Julia function. It looks just like the ODE, except in this case there is a function
h(p,t) which allows you to interpolate and grab previous values.

We must provide a history function h(p,t) that gives values for u before
t0. Here we assume that the solution was constant before the initial time point. Additionally, we pass
constant_lags = c(20.0) to tell the solver that only constant-time lags were used and what the lag length
was. This helps improve the solver accuracy by accurately stepping at the points of discontinuity. Together
this is:

f <- JuliaCall::julia_eval("function f(du, u, h, p, t)
  du[1] = 1.1/(1 + sqrt(10)*(h(p, t-20)[1])^(5/4)) - 10*u[1]/(1 + 40*u[2])
  du[2] = 100*u[1]/(1 + 40*u[2]) - 2.43*u[2]
end")
h <- JuliaCall::julia_eval("function h(p, t)
  [1.05767027/3, 1.030713491/3]
end")
u0 <- c(1.05767027/3, 1.030713491/3)
tspan <- c(0.0, 100.0)
constant_lags <- c(20.0)
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("tspan", tspan)
JuliaCall::julia_assign("constant_lags", tspan)
prob <- JuliaCall::julia_eval("DDEProblem(f, u0, h, tspan, constant_lags = constant_lags)")
sol <- de$solve(prob,de$MethodOfSteps(de$Tsit5()))
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |> plotly::add_trace(y = ~V2)

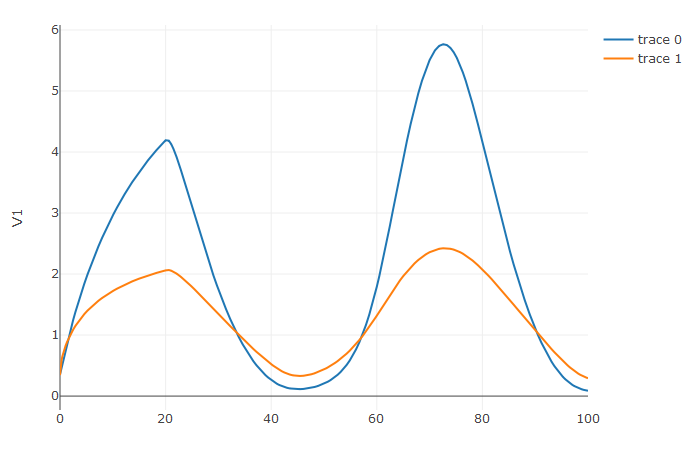
delay

Notice that the solver accurately is able to simulate the kink (discontinuity) at t=20 due to the discontinuity
of the derivative at the initial time point! This is why declaring discontinuities can enhance the solver accuracy.

GPU-Accelerated ODE Solving of Ensembles

In many cases one is interested in solving the same ODE many times over many
different initial conditions and parameters. In diffeqr parlance this is called
an ensemble solve. diffeqr inherits the parallelism tools of the
SciML ecosystem that are used for things like
automated equation discovery and acceleration.
Here we will demonstrate using these parallel tools to accelerate the solving
of an ensemble.

First, let’s define the JIT-accelerated Lorenz equation like before:

de <- diffeqr::diffeq_setup()
lorenz <- function (u,p,t){
  du1 = p[1]*(u[2]-u[1])
  du2 = u[1]*(p[2]-u[3]) - u[2]
  du3 = u[1]*u[2] - p[3]*u[3]
  c(du1,du2,du3)
}
u0 <- c(1.0,1.0,1.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(lorenz,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)

Now we use the EnsembleProblem as defined on the
ensemble parallelism page of the documentation:
Let’s build an ensemble by utilizing uniform random numbers to randomize the
initial conditions and parameters:

prob_func <- function (prob,i,rep){
  de$remake(prob,u0=runif(3)*u0,p=runif(3)*p)
}
ensembleprob = de$EnsembleProblem(fastprob, prob_func = prob_func, safetycopy=FALSE)

Now we solve the ensemble in serial:

sol = de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01)

To add GPUs to the mix, we need to bring in DiffEqGPU.
The diffeqr::diffeqgpu_setup() helper function will install CUDA for you and
bring all of the bindings into the returned object:

degpu <- diffeqr::diffeqgpu_setup("CUDA")

Note: `diffeqr::diffeqgpu_setup` can take awhile to run the first time as it installs the drivers!

Now we simply use EnsembleGPUKernel(degpu$CUDABackend()) with a
GPU-specialized ODE solver GPUTsit5() to solve 10,000 ODEs on the GPU in
parallel:

sol <- de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01)

For the full list of choices for specialized GPU solvers, see
the DiffEqGPU.jl documentation.

Note that EnsembleGPUArray can be used as well, like:

sol <- de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(degpu$CUDABackend()),trajectories=10000,saveat=0.01)

though we highly recommend the EnsembleGPUKernel methods for more speed. Given
the way the JIT compilation performed will also ensure that the faster kernel
generation methods work, EnsembleGPUKernel is almost certainly the
better choice in most applications.

Benchmark

To see how much of an effect the parallelism has, let’s test this against R’s
deSolve package. This is exactly the same problem as the documentation example
for deSolve, so let’s copy that verbatim and then add a function to do the
ensemble generation:

library(deSolve)
Lorenz <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
    dX <-  a * X + Y * Z
    dY <-  b * (Y - Z)
    dZ <- -X * Y + c * Y - Z
    list(c(dX, dY, dZ))
  })
}

parameters <- c(a = -8/3, b = -10, c = 28)
state      <- c(X = 1, Y = 1, Z = 1)
times      <- seq(0, 100, by = 0.01)
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)

lorenz_solve <- function (i){
  state      <- c(X = runif(1), Y = runif(1), Z = runif(1))
  parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
  out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
}

Using lapply to generate the ensemble we get:

> system.time({ lapply(1:1000,lorenz_solve) })
   user  system elapsed
 225.81    0.46  226.63

Now let’s see how the JIT-accelerated serial Julia version stacks up against that:

> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=1000,saveat=0.01) })
   user  system elapsed
   2.75    0.30    3.08

Julia is already about 73x faster than the pure R solvers here! Now let’s add
GPU-acceleration to the mix:

> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=1000,saveat=0.01) })
   user  system elapsed 
   0.11    0.00    0.12

Already 26x times faster! But the GPU acceleration is made for massively
parallel problems, so let’s up the trajectories a bit. We will not use more
trajectories from R because that would take too much computing power, so let’s
see what happens to the Julia serial and GPU at 10,000 trajectories:

> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01) })
   user  system elapsed
  35.02    4.19   39.25

> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01) })
   user  system elapsed 
   1.22    0.23    1.50

To compare this to the pure Julia code:

using OrdinaryDiffEq, DiffEqGPU, CUDA, StaticArrays
function lorenz(u, p, t)
    σ = p[1]
    ρ = p[2]
    β = p[3]
    du1 = σ * (u[2] - u[1])
    du2 = u[1] * (ρ - u[3]) - u[2]
    du3 = u[1] * u[2] - β * u[3]
    return SVector{3}(du1, du2, du3)
end

u0 = SA[1.0f0; 0.0f0; 0.0f0]
tspan = (0.0f0, 10.0f0)
p = SA[10.0f0, 28.0f0, 8 / 3.0f0]
prob = ODEProblem{false}(lorenz, u0, tspan, p)
prob_func = (prob, i, repeat) -> remake(prob, p = (@SVector rand(Float32, 3)) .* p)
monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy = false)
@time sol = solve(monteprob, GPUTsit5(), EnsembleGPUKernel(CUDA.CUDABackend()),
    trajectories = 10_000,
    saveat = 1.0f0);

# 0.015064 seconds (257.68 k allocations: 13.132 MiB)

which is about two orders of magnitude faster for computing 10,000 trajectories,
note that the major factors are that we cannot define 32-bit floating point values
from R and the prob_func for generating the initial conditions and parameters
is a major bottleneck since this function is written in R.

To see how this scales in Julia, let’s take it to insane heights. First, let’s
reduce the amount we’re saving:

@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=10_000,saveat=1.0f0)
0.015040 seconds (257.64 k allocations: 13.130 MiB)

This highlights that controlling memory pressure is key with GPU usage: you will
get much better performance when requiring less saved points on the GPU.

@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=100_000,saveat=1.0f0)
# 0.150901 seconds (2.60 M allocations: 131.576 MiB)

compared to serial:

@time sol = solve(monteprob,Tsit5(),EnsembleSerial(),trajectories=100_000,saveat=1.0f0)
# 22.136743 seconds (16.40 M allocations: 1.628 GiB, 42.98% gc time)

And now we start to see that scaling power! Let’s solve 1 million trajectories:

@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=1_000_000,saveat=1.0f0)
# 1.031295 seconds (3.40 M allocations: 241.075 MiB)

For reference, let’s look at deSolve with the change to only save that much:

times      <- seq(0, 100, by = 1.0)
lorenz_solve <- function (i){
  state      <- c(X = runif(1), Y = runif(1), Z = runif(1))
  parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
  out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
}

system.time({ lapply(1:1000,lorenz_solve) })

   user  system elapsed 
  49.69    3.36   53.42

The GPU version is solving 1000x as many trajectories, 50x as fast! So conclusion,
if you need the most speed, you may want to move to the Julia version to get the
most out of your GPU due to Float32’s, and when using GPUs make sure it’s a problem
with a relatively average or low memory pressure, and these methods will give
orders of magnitude acceleration compared to what you might be used to.

diffeqr

diffeqr

Installation

Google Collab Notebooks

Usage

Ordinary Differential Equation (ODE) Examples

1D Linear ODEs

Systems of ODEs

Option Handling

Performance Enhancements

Limitations of the JIT Compilation

Stochastic Differential Equation (SDE) Examples

1D SDEs

Systems of Diagonal Noise SDEs

Systems of SDEs with Non-Diagonal Noise

Differential-Algebraic Equation (DAE) Examples

Delay Differential Equation (DDE) Examples

GPU-Accelerated ODE Solving of Ensembles

Note: diffeqr::diffeqgpu_setup can take awhile to run the first time as it installs the drivers!

Benchmark

Note: `diffeqr::diffeqgpu_setup` can take awhile to run the first time as it installs the drivers!