A Python toolkit/library for reality-centric machine/deep learning and data mining on partially-observed time series, including SOTA neural network models for scientific analysis tasks of imputation/classification/clustering/forecasting/anomaly detection/cleaning on incomplete industrial (irregularly-sampled) multivariate TS with NaN missing values
Welcome to PyPOTS
a Python toolbox for machine learning on Partially-Observed Time Series
⦿ Motivation: Due to all kinds of reasons like failure of collection sensors, communication error,
and unexpected malfunction, missing values are common to see in time series from the real-world environment.
This makes partially-observed time series (POTS) a pervasive problem in open-world modeling and prevents advanced
data analysis. Although this problem is important, the area of machine learning on POTS still lacks a dedicated toolkit.
PyPOTS is created to fill in this blank.
⦿ Mission: PyPOTS (pronounced “Pie Pots”) is born to become a handy toolbox that is going to make machine learning on
POTS easy rather than tedious, to help engineers and researchers focus more on the core problems in their hands rather
than on how to deal with the missing parts in their data. PyPOTS will keep integrating classical and the latest
state-of-the-art machine learning algorithms for partially-observed multivariate time series. For sure, besides various
algorithms, PyPOTS is going to have unified APIs together with detailed documentation and interactive examples across
algorithms as tutorials.
🤗 Please star this repo to help others notice PyPOTS if you think it is a useful toolkit.
Please kindly cite PyPOTS in your publications if it helps with
your research.
This really means a lot to our open-source research. Thank you!
The rest of this readme file is organized as follows:
❖ Available Algorithms,
❖ PyPOTS Ecosystem,
❖ Installation,
❖ Usage,
❖ Citing PyPOTS,
❖ Contribution,
❖ Community.
❖ Available Algorithms
PyPOTS supports imputation, classification, clustering, forecasting, and anomaly detection tasks on multivariate
partially-observed time series with missing values. The table below shows the availability of each algorithm
(sorted by Year) in PyPOTS for different tasks. The symbol ✅ indicates the algorithm is available for the
corresponding task (note that models will be continuously updated in the future to handle tasks that are not
currently supported. Stay tuned❗️).
🌟 Since v0.2, all neural-network models in PyPOTS has got hyperparameter-optimization support.
This functionality is implemented with the Microsoft NNI framework. You may want to
refer to our time-series imputation survey and benchmark
repo Awesome_Imputation
to see how to config and tune the hyperparameters.
🔥 Note that all models whose name with 🧑🔧 in the table (e.g. Transformer, iTransformer, Informer etc.) are not
originally proposed as algorithms for POTS data in their papers, and they cannot directly accept time series with
missing values as input, let alone imputation. To make them applicable to POTS data, we specifically apply the
embedding strategy and training approach (ORT+MIT) the same as we did in
the SAITS paper[1].
The task types are abbreviated as follows:
IMPU: Imputation;
FORE: Forecasting;
CLAS: Classification;
CLUS: Clustering;
ANOD: Anomaly Detection.
In addition to the 5 tasks, PyPOTS also provides TS2Vec[2] for time series representation learning and vectorization.
The paper references and links are all listed at the bottom of this file.
| Type | Algo | IMPU | FORE | CLAS | CLUS | ANOD | Year - Venue |
|---|---|---|---|---|---|---|---|
| LLM&TSFM | ✅ | ✅ | ✅ | ✅ | ✅ | Join waitlist | |
| Neural Net | TimeMixer++[4] | ✅ | ✅ | 2025 - ICLR |
|||
| LLM | Time-LLM🧑🔧[5] | ✅ | ✅ | 2024 - ICLR |
|||
| TSFM | MOMENT[6] | ✅ | ✅ | 2024 - ICML |
|||
| Neural Net | TSLANet[7] | ✅ | 2024 - ICML |
||||
| Neural Net | TEFN🧑🔧[8] | ✅ | ✅ | ✅ | ✅ | 2024 - arXiv |
|
| Neural Net | FITS🧑🔧[9] | ✅ | ✅ | 2024 - ICLR |
|||
| Neural Net | TimeMixer[10] | ✅ | ✅ | ✅ | 2024 - ICLR |
||
| Neural Net | iTransformer🧑🔧[11] | ✅ | ✅ | ✅ | 2024 - ICLR |
||
| Neural Net | ModernTCN[12] | ✅ | ✅ | 2024 - ICLR |
|||
| Neural Net | ImputeFormer🧑🔧[13] | ✅ | ✅ | 2024 - KDD |
|||
| Neural Net | TOTEM [14] | ✅ | 2024 - TMLR |
||||
| Neural Net | SAITS[1:1] | ✅ | ✅ | ✅ | 2023 - ESWA |
||
| LLM | GPT4TS[15] | ✅ | ✅ | 2023 - NeurIPS |
|||
| Neural Net | FreTS🧑🔧[16] | ✅ | 2023 - NeurIPS |
||||
| Neural Net | Koopa🧑🔧[17] | ✅ | 2023 - NeurIPS |
||||
| Neural Net | Crossformer🧑🔧[18] | ✅ | ✅ | 2023 - ICLR |
|||
| Neural Net | TimesNet[19] | ✅ | ✅ | ✅ | ✅ | 2023 - ICLR |
|
| Neural Net | PatchTST🧑🔧[20] | ✅ | ✅ | ✅ | 2023 - ICLR |
||
| Neural Net | ETSformer🧑🔧[21] | ✅ | ✅ | 2023 - ICLR |
|||
| Neural Net | MICN🧑🔧[22] | ✅ | ✅ | 2023 - ICLR |
|||
| Neural Net | DLinear🧑🔧[23] | ✅ | ✅ | ✅ | 2023 - AAAI |
||
| Neural Net | TiDE🧑🔧[24] | ✅ | 2023 - TMLR |
||||
| Neural Net | CSAI[25] | ✅ | ✅ | 2023 - arXiv |
|||
| Neural Net | SegRNN🧑🔧[26] | ✅ | ✅ | ✅ | 2023 - arXiv |
||
| Neural Net | TS2Vec[2:1] | ✅ | 2022 - AAAI |
||||
| Neural Net | SCINet🧑🔧[27] | ✅ | ✅ | 2022 - NeurIPS |
|||
| Neural Net | Nonstationary Tr.🧑🔧[28] | ✅ | ✅ | 2022 - NeurIPS |
|||
| Neural Net | FiLM🧑🔧[29] | ✅ | ✅ | ✅ | 2022 - NeurIPS |
||
| Neural Net | RevIN_SCINet🧑🔧[30] | ✅ | 2022 - ICLR |
||||
| Neural Net | Pyraformer🧑🔧[31] | ✅ | ✅ | 2022 - ICLR |
|||
| Neural Net | Raindrop[32] | ✅ | 2022 - ICLR |
||||
| Neural Net | FEDformer🧑🔧[33] | ✅ | ✅ | 2022 - ICML |
|||
| Neural Net | Autoformer🧑🔧[34] | ✅ | ✅ | ✅ | 2021 - NeurIPS |
||
| Neural Net | CSDI[35] | ✅ | ✅ | 2021 - NeurIPS |
|||
| Neural Net | Informer🧑🔧[36] | ✅ | ✅ | 2021 - AAAI |
|||
| Neural Net | US-GAN[37] | ✅ | 2021 - AAAI |
||||
| Neural Net | CRLI[38] | ✅ | 2021 - AAAI |
||||
| Probabilistic | BTTF[39] | ✅ | 2021 - TPAMI |
||||
| Neural Net | StemGNN🧑🔧[40] | ✅ | 2020 - NeurIPS |
||||
| Neural Net | Reformer🧑🔧[41] | ✅ | ✅ | 2020 - ICLR |
|||
| Neural Net | GP-VAE[42] | ✅ | 2020 - AISTATS |
||||
| Neural Net | VaDER[43] | ✅ | 2019 - GigaSci. |
||||
| Neural Net | M-RNN[44] | ✅ | 2019 - TBME |
||||
| Neural Net | BRITS[45] | ✅ | ✅ | 2018 - NeurIPS |
|||
| Neural Net | GRU-D[46] | ✅ | ✅ | 2018 - Sci. Rep. |
|||
| Neural Net | TCN🧑🔧[47] | ✅ | 2018 - arXiv |
||||
| Neural Net | Transformer🧑🔧[48] | ✅ | ✅ | ✅ | 2017 - NeurIPS |
||
| MF | TRMF[49] | ✅ | 2016 - NeurIPS |
||||
| Naive | Lerp[50] | ✅ | |||||
| Naive | LOCF/NOCB | ✅ | |||||
| Naive | Mean | ✅ | |||||
| Naive | Median | ✅ |
🙋 Differences between LLM (Large Language Model) and TSFM (Time-Series Foundation Model) in the above table:
LLM refers to the models that are pre-trained on large-scale text data and can be fine-tuned for specific tasks.
TSFM refers to the models that are pre-trained on large-scale time series data, inspired by recent achievements
of foundation models in CV and NLP.
💯 Contribute your model right now to increase your research impact! PyPOTS downloads are increasing rapidly
(1M+ in total and 2k+ daily on PyPI so far),
and your work will be widely used and cited by the community.
Refer to the contribution guide to see how to include your model in
PyPOTS.
❖ PyPOTS Ecosystem
At PyPOTS, things are related to coffee, which we’re familiar with. Yes, this is a coffee universe!
As you can see, there is a coffee pot in the PyPOTS logo. And what else? Please read on 😉
👈 Time series datasets are taken as coffee beans at PyPOTS, and POTS datasets are incomplete coffee beans with missing
parts that have their own meanings. To make various public time-series datasets readily available to users,
Time Series Data Beans (TSDB) is created to make loading time-series datasets super easy!
Visit TSDB right now to know more about this handy tool 🛠, and it now supports a
total of 172 open-source datasets!
👉 To simulate the real-world data beans with missingness, the ecosystem library
PyGrinder, a toolkit helping grind your coffee beans into incomplete ones, is
created. Missing patterns fall into three categories according to Robin’s theory[51]:
MCAR (missing completely at random), MAR (missing at random), and MNAR (missing not at random).
PyGrinder supports all of them and additional functionalities related to missingness.
With PyGrinder, you can introduce synthetic missing values into your datasets with a single line of code.
👈 To fairly evaluate the performance of PyPOTS algorithms, the benchmarking suite
BenchPOTS is created, which provides standard and unified data-preprocessing
pipelines to prepare datasets for measuring the performance of different POTS algorithms on various tasks.
👉 Now the beans, grinder, and pot are ready, please have a seat on the bench and let’s think about how to brew us a cup
of coffee. Tutorials are necessary! Considering the future workload, PyPOTS tutorials are released in a single repo,
and you can find them in BrewPOTS.
Take a look at it now, and learn how to brew your POTS datasets!
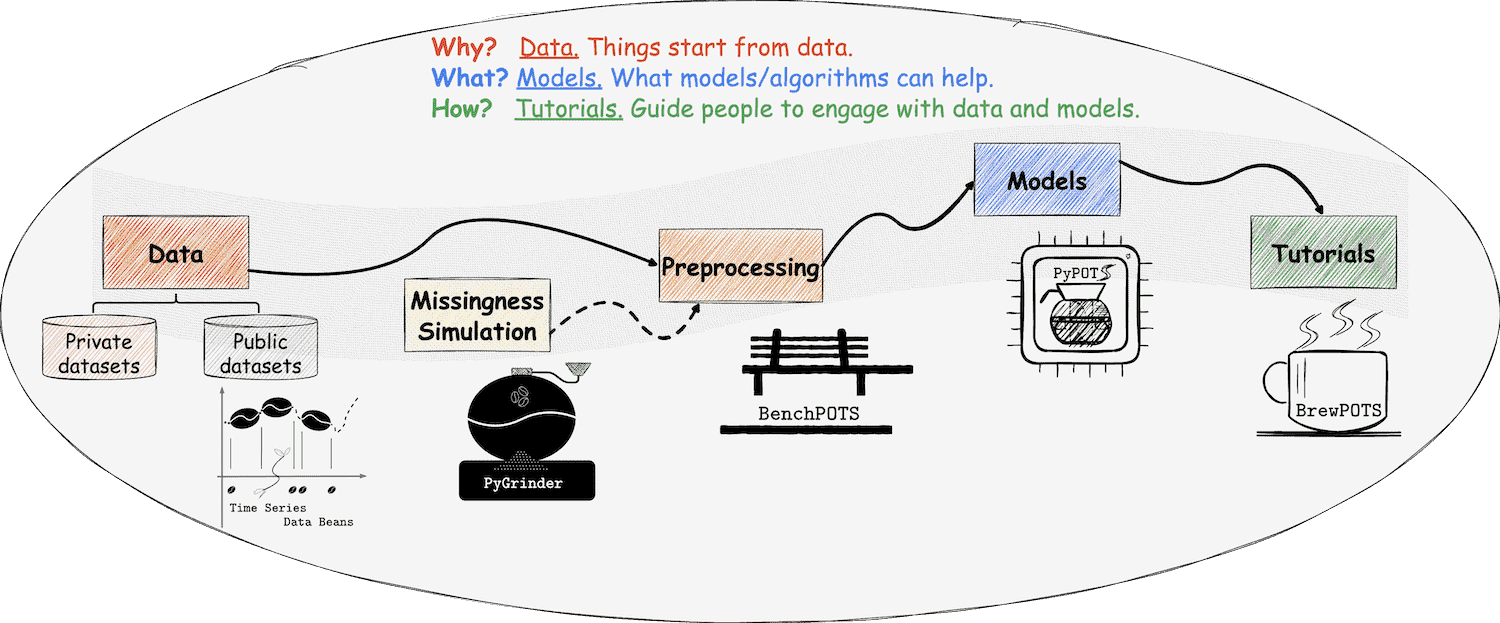
☕️ Welcome to the universe of PyPOTS. Enjoy it and have fun!
❖ Installation
You can refer to the installation instruction in PyPOTS documentation
for a guideline with more details.
PyPOTS is available on both PyPI
and Anaconda.
You can install PyPOTS like below as well as
TSDB,PyGrinder,
BenchPOTS, and AI4TS:
# via pip
pip install pypots # the first time installation
pip install pypots --upgrade # update pypots to the latest version
# install from the latest source code with the latest features but may be not officially released yet
pip install https://github.com/WenjieDu/PyPOTS/archive/main.zip
# via conda
conda install conda-forge::pypots # the first time installation
conda update conda-forge::pypots # update pypots to the latest version
# via docker
docker run -it --name pypots wenjiedu/pypots # docker will auto pull our built image and run a instance for you
# after things settled, you can run python in the container to access the well-configured environment for running pypots
# if you'd like to detach from the container, press ctrl-P + ctrl-Q
# run `docker attach pypots` to enter the container again.
❖ Usage
Besides BrewPOTS, you can also find a simple and quick-start tutorial notebook
on Google Colab
. If you have further questions, please refer to PyPOTS documentation docs.pypots.com.
You can also raise an issue or ask in our community.
We present you a usage example of imputing missing values in time series with PyPOTS below, you can click it to view.
Click here to see an example applying SAITS on PhysioNet2012 for imputation:
import numpy as np
from sklearn.preprocessing import StandardScaler
from pygrinder import mcar, calc_missing_rate
from benchpots.datasets import preprocess_physionet2012
data = preprocess_physionet2012(subset='set-a',rate=0.1) # Our ecosystem libs will automatically download and extract it
train_X, val_X, test_X = data["train_X"], data["val_X"], data["test_X"]
print(train_X.shape) # (n_samples, n_steps, n_features)
print(val_X.shape) # samples (n_samples) in train set and val set are different, but they have the same sequence len (n_steps) and feature dim (n_features)
print(f"We have {calc_missing_rate(train_X):.1%} values missing in train_X")
train_set = {"X": train_X} # in training set, simply put the incomplete time series into it
val_set = {
"X": val_X,
"X_ori": data["val_X_ori"], # in validation set, we need ground truth for evaluation and picking the best model checkpoint
}
test_set = {"X": test_X} # in test set, only give the testing incomplete time series for model to impute
test_X_ori = data["test_X_ori"] # test_X_ori bears ground truth for evaluation
indicating_mask = np.isnan(test_X) ^ np.isnan(test_X_ori) # mask indicates the values that are missing in X but not in X_ori, i.e. where the gt values are
from pypots.imputation import SAITS # import the model you want to use
from pypots.nn.functional import calc_mae
saits = SAITS(n_steps=train_X.shape[1], n_features=train_X.shape[2], n_layers=2, d_model=256, n_heads=4, d_k=64, d_v=64, d_ffn=128, dropout=0.1, epochs=5)
saits.fit(train_set, val_set) # train the model on the dataset
imputation = saits.impute(test_set) # impute the originally-missing values and artificially-missing values
mae = calc_mae(imputation, np.nan_to_num(test_X_ori), indicating_mask) # calculate mean absolute error on the ground truth (artificially-missing values)
saits.save("save_it_here/saits_physionet2012.pypots") # save the model for future use
saits.load("save_it_here/saits_physionet2012.pypots") # reload the serialized model file for following imputation or training
❖ Citing PyPOTS
[!TIP]
[Updates in Jun 2024] 😎 The 1st comprehensive time-seres imputation benchmark paper
TSI-Bench: Benchmarking Time Series Imputation now is public available.
The code is open source in the repo Awesome_Imputation.
With nearly 35,000 experiments, we provide a comprehensive benchmarking study on 28 imputation methods, 3 missing
patterns (points, sequences, blocks),
various missing rates, and 8 real-world datasets.[Updates in Feb 2024] 🎉 Our survey
paper Deep Learning for Multivariate Time Series Imputation: A Survey has been
released on arXiv.
We comprehensively review the literature of the state-of-the-art deep-learning imputation methods for time series,
provide a taxonomy for them, and discuss the challenges and future directions in this field.
The paper introducing PyPOTS is available on arXiv,
and a short version of it is accepted by the 9th SIGKDD international workshop on Mining and Learning from Time
Series (MiLeTS’23)).
Additionally, PyPOTS has been included as a PyTorch Ecosystem project.
We are pursuing to publish it in prestigious academic venues, e.g. JMLR (track for
Machine Learning Open Source Software). If you use PyPOTS in your work,
please cite it as below and 🌟star this repository to make others notice this library. 🤗
There are scientific research projects using PyPOTS and referencing in their papers.
Here is an incomplete list of them.
@article{du2023pypots,
title = {{PyPOTS: a Python toolbox for data mining on Partially-Observed Time Series}},
author = {Wenjie Du},
journal = {arXiv preprint arXiv:2305.18811},
year = {2023},
}
or
Wenjie Du.
PyPOTS: a Python toolbox for data mining on Partially-Observed Time Series.
arXiv, abs/2305.18811, 2023.
❖ Contribution
You’re very welcome to contribute to this exciting project!
By committing your code, you’ll
- make your well-established model out-of-the-box for PyPOTS users to run,
and help your work obtain more exposure and impact.
Take a look at our inclusion criteria.
You can utilize thetemplatefolder in each task package (e.g.
pypots/imputation/template) to quickly
start; - become one of PyPOTS contributors and
be listed as a volunteer developer on the PyPOTS website; - get mentioned in PyPOTS release notes;
You can also contribute to PyPOTS by simply staring🌟 this repo to help more people notice it.
Your star is your recognition to PyPOTS, and it matters!
👏 Click here to view PyPOTS stargazers and forkers.
We're so proud to have more and more awesome users, as well as more bright ✨stars:
👀 Check out a full list of our users’ affiliations on PyPOTS website here!
❖ Community
We care about the feedback from our users, so we’re building PyPOTS community on
- Slack. General discussion,
Q&A, and our development team are here; - LinkedIn. Official announcements and news are here;
- WeChat (微信公众号). We also run a group chat on WeChat,
and you can get the QR code from the official account after following it;
If you have any suggestions or want to contribute ideas or share time-series related papers, join us and tell.
PyPOTS community is open, transparent, and surely friendly. Let’s work together to build and improve PyPOTS!
Du, W., Cote, D., & Liu, Y. (2023).
SAITS: Self-Attention-based Imputation for Time Series.
Expert systems with applications. ↩︎ ↩︎Yue, Z., Wang, Y., Duan, J., Yang, T., Huang, C., Tong, Y., & Xu, B. (2022).
TS2Vec: Towards Universal Representation of Time Series.
AAAI 2022. ↩︎ ↩︎Project Gungnir, the world 1st LLM for time-series multitask modeling, will meet you soon. 🚀 Missing values and
variable lengths in your datasets?
Hard to perform multitask learning with your time series? Not problems no longer. We’ll open application for public beta
test recently 😉 Follow us, and stay tuned!
Time-Series.AI ↩︎Wang, S., Li, J., Shi, X., Ye, Z., Mo, B., Lin, W., Ju, S., Chu, Z. & Jin, M. (2025).
TimeMixer++: A General Time Series Pattern Machine for Universal Predictive Analysis.
ICLR 2025. ↩︎Jin, M., Wang, S., Ma, L., Chu, Z., Zhang, J. Y., Shi, X., … & Wen, Q. (2024).
Time-LLM: Time Series Forecasting by Reprogramming Large Language Models.
ICLR 2024. ↩︎Goswami, M., Szafer, K., Choudhry, A., Cai, Y., Li, S., & Dubrawski, A. (2024).
MOMENT: A Family of Open Time-series Foundation Models.
ICML 2024. ↩︎Eldele, E., Ragab, M., Chen, Z., Wu, M., & Li, X. (2024).
TSLANet: Rethinking Transformers for Time Series Representation Learning.
ICML 2024. ↩︎Zhan, T., He, Y., Deng, Y., Li, Z., Du, W., & Wen, Q. (2024).
Time Evidence Fusion Network: Multi-source View in Long-Term Time Series Forecasting.
arXiv 2024. ↩︎Xu, Z., Zeng, A., & Xu, Q. (2024).
FITS: Modeling Time Series with 10k parameters.
ICLR 2024. ↩︎Wang, S., Wu, H., Shi, X., Hu, T., Luo, H., Ma, L., … & ZHOU, J. (2024).
TimeMixer: Decomposable Multiscale Mixing for Time Series Forecasting.
ICLR 2024. ↩︎Liu, Y., Hu, T., Zhang, H., Wu, H., Wang, S., Ma, L., & Long, M. (2024).
iTransformer: Inverted Transformers Are Effective for Time Series Forecasting.
ICLR 2024. ↩︎Luo, D., & Wang X. (2024).
ModernTCN: A Modern Pure Convolution Structure for General Time Series Analysis.
ICLR 2024. ↩︎Nie, T., Qin, G., Mei, Y., & Sun, J. (2024).
ImputeFormer: Low Rankness-Induced Transformers for Generalizable Spatiotemporal Imputation.
KDD 2024. ↩︎Talukder, S., Yue, Y., & Gkioxari, G. (2024).
TOTEM: TOkenized Time Series EMbeddings for General Time Series Analysis.
TMLR 2024. ↩︎Zhou, T., Niu, P., Sun, L., & Jin, R. (2023).
One Fits All: Power General Time Series Analysis by Pretrained LM.
NeurIPS 2023. ↩︎Yi, K., Zhang, Q., Fan, W., Wang, S., Wang, P., He, H., An, N., Lian, D., Cao, L., & Niu, Z. (2023).
Frequency-domain MLPs are More Effective Learners in Time Series Forecasting.
NeurIPS 2023. ↩︎Liu, Y., Li, C., Wang, J., & Long, M. (2023).
Koopa: Learning Non-stationary Time Series Dynamics with Koopman Predictors.
NeurIPS 2023. ↩︎Zhang, Y., & Yan, J. (2023).
Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting.
ICLR 2023. ↩︎Wu, H., Hu, T., Liu, Y., Zhou, H., Wang, J., & Long, M. (2023).
TimesNet: Temporal 2d-variation modeling for general time series analysis.
ICLR 2023 ↩︎Nie, Y., Nguyen, N. H., Sinthong, P., & Kalagnanam, J. (2023).
A time series is worth 64 words: Long-term forecasting with transformers.
ICLR 2023 ↩︎Woo, G., Liu, C., Sahoo, D., Kumar, A., & Hoi, S. (2023).
ETSformer: Exponential Smoothing Transformers for Time-series Forecasting.
ICLR 2023 ↩︎Wang, H., Peng, J., Huang, F., Wang, J., Chen, J., & Xiao, Y. (2023).
MICN: Multi-scale Local and Global Context Modeling for Long-term Series Forecasting.
ICLR 2023. ↩︎Zeng, A., Chen, M., Zhang, L., & Xu, Q. (2023).
Are transformers effective for time series forecasting?.
AAAI 2023 ↩︎Das, A., Kong, W., Leach, A., Mathur, S., Sen, R., & Yu, R. (2023).
Long-term Forecasting with TiDE: Time-series Dense Encoder.
TMLR 2023. ↩︎Qian, L., Ibrahim, Z., Ellis, H. L., Zhang, A., Zhang, Y., Wang, T., & Dobson, R. (2023).
Knowledge Enhanced Conditional Imputation for Healthcare Time-series.
arXiv 2023. ↩︎Lin, S., Lin, W., Wu, W., Zhao, F., Mo, R., & Zhang, H. (2023).
SegRNN: Segment Recurrent Neural Network for Long-Term Time Series Forecasting.
arXiv 2023. ↩︎Liu, M., Zeng, A., Chen, M., Xu, Z., Lai, Q., Ma, L., & Xu, Q. (2022).
SCINet: Time Series Modeling and Forecasting with Sample Convolution and Interaction.
NeurIPS 2022. ↩︎Liu, Y., Wu, H., Wang, J., & Long, M. (2022).
Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting.
NeurIPS 2022. ↩︎Zhou, T., Ma, Z., Wen, Q., Sun, L., Yao, T., Yin, W., & Jin, R. (2022).
FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forecasting.
NeurIPS 2022. ↩︎Kim, T., Kim, J., Tae, Y., Park, C., Choi, J. H., & Choo, J. (2022).
Reversible Instance Normalization for Accurate Time-Series Forecasting against Distribution Shift.
ICLR 2022. ↩︎Liu, S., Yu, H., Liao, C., Li, J., Lin, W., Liu, A. X., & Dustdar, S. (2022).
Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting.
ICLR 2022. ↩︎Zhang, X., Zeman, M., Tsiligkaridis, T., & Zitnik, M. (2022).
Graph-Guided Network for Irregularly Sampled Multivariate Time Series.
ICLR 2022. ↩︎Zhou, T., Ma, Z., Wen, Q., Wang, X., Sun, L., & Jin, R. (2022).
FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting.
ICML 2022. ↩︎Wu, H., Xu, J., Wang, J., & Long, M. (2021).
Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting.
NeurIPS 2021. ↩︎Tashiro, Y., Song, J., Song, Y., & Ermon, S. (2021).
CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation.
NeurIPS 2021. ↩︎Zhou, H., Zhang, S., Peng, J., Zhang, S., Li, J., Xiong, H., & Zhang, W. (2021).
Informer: Beyond efficient transformer for long sequence time-series forecasting.
AAAI 2021. ↩︎Miao, X., Wu, Y., Wang, J., Gao, Y., Mao, X., & Yin, J. (2021).
Generative Semi-supervised Learning for Multivariate Time Series Imputation.
AAAI 2021. ↩︎Ma, Q., Chen, C., Li, S., & Cottrell, G. W. (2021).
Learning Representations for Incomplete Time Series Clustering.
AAAI 2021. ↩︎Chen, X., & Sun, L. (2021).
Bayesian Temporal Factorization for Multidimensional Time Series Prediction.
IEEE transactions on pattern analysis and machine intelligence. ↩︎Cao, D., Wang, Y., Duan, J., Zhang, C., Zhu, X., Huang, C., Tong, Y., Xu, B., Bai, J., Tong, J., & Zhang, Q. (
2020).
Spectral Temporal Graph Neural Network for Multivariate Time-series Forecasting.
NeurIPS 2020. ↩︎Kitaev, N., Kaiser, Ł., & Levskaya, A. (2020).
Reformer: The Efficient Transformer.
ICLR 2020. ↩︎Fortuin, V., Baranchuk, D., Raetsch, G. & Mandt, S. (2020).
GP-VAE: Deep Probabilistic Time Series Imputation.
AISTATS 2020. ↩︎Jong, J.D., Emon, M.A., Wu, P., Karki, R., Sood, M., Godard, P., Ahmad, A., Vrooman, H.A., Hofmann-Apitius, M., &
Fröhlich, H. (2019).
Deep learning for clustering of multivariate clinical patient trajectories with missing values.
GigaScience. ↩︎Yoon, J., Zame, W. R., & van der Schaar, M. (2019).
Estimating Missing Data in Temporal Data Streams Using Multi-Directional Recurrent Neural Networks.
IEEE Transactions on Biomedical Engineering. ↩︎Cao, W., Wang, D., Li, J., Zhou, H., Li, L., & Li, Y. (2018).
BRITS: Bidirectional Recurrent Imputation for Time Series.
NeurIPS 2018. ↩︎Che, Z., Purushotham, S., Cho, K., Sontag, D.A., & Liu, Y. (2018).
Recurrent Neural Networks for Multivariate Time Series with Missing Values.
Scientific Reports. ↩︎Bai, S., Kolter, J. Z., & Koltun, V. (2018).
An empirical evaluation of generic convolutional and recurrent networks for sequence modeling.
arXiv 2018. ↩︎Vaswani, A., Shazeer, N.M., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L., & Polosukhin, I. (
2017).
Attention is All you Need.
NeurIPS 2017. ↩︎Yu, H. F., Rao, N., & Dhillon, I. S. (2016).
Temporal regularized matrix factorization for high-dimensional time series prediction.
NeurIPS 2016. ↩︎Rubin, D. B. (1976).
Inference and missing data.
Biometrika. ↩︎














